O objetivo aqui é apresentar como podemos usar uma rede neural para tomadas de decisão. No caso deste artigo a rede neural deverá decidir se o robô deve virar para a esquerda, seguir em frente, ou virar para a direita, tendo como input sensores que irão indicar se existe caminho à esquerda, a frente, ou à direita.
O grupo VisioRob está testando uma ferramenta a Unity 3D para simulação e controle de robôs. Dessa forma utilizamos essa ferramenta para o desenvolvimento de um simulador onde temos um robô que irá se mover, utilizando uma rede neural para a tomada de decisões. A rede neural deverá ser treinada em outro ambiente e os seus pesos e bias informados para o simulador. Neste artigo irmos será demonstrado o simulador e como podemos treinar uma rede neural para o simulador.
Acesse o simulador por este link
Introdução sobre redes neurais
Podemos interpretar uma rede neural como um conjunto de neurônios que se ligam de tal forma que podemos treinar esta estrutura para que ela possa tomar algumas decisões baseadas em estímulos que ela recebe. Já o neurônio, que foi mencionado anteriormente, é a unidade básica de uma rede neural. Ele é responsável por receber estímulos e processar esses estímulos em suas características. A estrutura básica de uma rede neural é o que está apresentado na Figura 1.
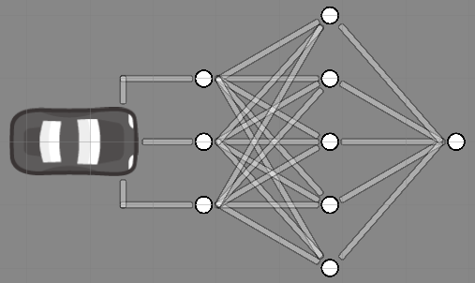
Os círculos brancos na Figura 1 são os neurônios, eles se ligam de forma a construírem a rede neural. O funcionamento de um neurônio pode ser descrito como:
A equação do neurônio indica que o resultado dele, o valor de a, depende da combinação dos valores que ele recebe como entrada. Os valores de entrada são representados pelo \sum_{i=1}^{n}w_ix_i, em que x_i representa um conjunto de valores informados pelos neurônios ligados a este e w_i representa o quanto cada neurônio anterior irá influenciar no resultado deste neurônio. Para colaborar com o resultado ainda temos o valor b_0 que representa o bias, que podemos considerar como um desvio médio acrescentado ao desempenho do neurônio.
Por fim, o neurônio pega o resultado e aplica à uma função de ativação, a função f(), que é responsável por fazer com que o comportamento do neurônio seja não linear. Sem essa função de ativação o resultado da rede neural seria uma combinação linear de todos os neurônios, o que impediria de que a rede neural trabalhasse de forma não linear. Existem vários modelos de função de ativação comumente utilizados em redes neurais.
Agora que temos uma ideia de como as redes neurais artificiais são descritas matematicamente, vamos verificar como podemos utilizar uma em um sistema de controle para um robô.
Rede neural do simulador do robô
Para o controle do robô, o simulador utiliza a rede neural apresentada na Figura 1. Conforme apresentado nela o robô possui três sensores, um para identificar se é possível ir para esquerda, um para identificar se é possível ir para frente e um para identificar se é possível ir para direita. Estes sensores estão ligados no que chamamos de camada de entrada ou input layer.
O movimento do robô irá depender do resultado da camada de saída ou output layer. No caso da Figura 1 podemos identificar a camada de saída sendo o neurônio que está mais a direita. Neste simulador o robô irá virar para a direita se o valor do ultimo neurônio for maior do que +0,5; irá virar para a esquerda se o valor do ultimo neurônio for menor do que -0,5; e, por fim, irá seguir em frente se o valor do ultimo neurônio estiver entre -0,5 e +0,5.
Qualquer conjunto de neurônios que estejam entre a camada de entrada e a camada de saída é o que consideramos como as camadas ocultas ou hidden layer. Conforme apresentado na Figura 1, a rede neural do simulador apresenta apenas uma única camada oculta. Para o problema apresentado ela será o suficiente. Dependendo do problema pode ser necessário adicionar mais camadas ocultas.
Veja que o neurônio da saída deverá fornecer um valor maior do que 0,5 até um valor menor do que -0,5. Para facilitar, vamos descrever que os valores da saída deverão estar entre -1 e +1. Dessa forma, podemos utilizar, como função de ativação, a função Tangente Hiperbólica, que é uma função matemática que fornece valores ente -1 e +1. A equação da Tangente Hiperbólica é descrita como:
f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}Para o simulador, a função de ativação Tangente Hiperbólica será utilizada tanto na camada de saída como na camada oculta. A camada de entrada não precisa de uma função de ativação, já que ela irá trabalhar com os valores recebidos dos sensores.
Agora conhecemos a rede neural do robô, mais isso não é o suficiente para fazer ele possa tomar decisões. Precisamos, agora treinar a rede neural para que ela possa, de certa forma, “aprender” como orientar o robô. Para realizarmos o treinamento, vamos construir uma rede neural equivalente à do robô em um ambiente que possamos treinar ela.
Construindo uma rede neural como a do robô utilizando o TensorFlow
O TensorFlow é uma biblioteca em Python que ajuda a criar e treinar redes neurais artificiais. Também recomendo o uso da plataforma Google Colab pois ela já vem com diversas bibliotecas instaladas e deixamos o peso computacional para os computadores do Google lidarem com eles.
Como vamos usar Python, vamos começar importando as bibliotecas que vamos utilizar. Podemos fazer isso usando os comandos:
import tensorflow as tf from matplotlib import pyplot as plt import numpy as np
Agora podemos usar o TensorFlow com tf, gerarmos gráficos com plt e trabalhar com vetores utilizando np.
Vamos, agora, criarmos uma rede neural idêntica à do simulador utilizando o TensorFlow. Para isso vamos utilizar os comandos:
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=5, activation="tanh",
input_shape=(3,),
name="Hidden_Layer",
),
tf.keras.layers.Dense(units=1, activation="tanh",
name="Output_Layer",
)
])
Agora a nossa rede neural está armazenada no objeto model. O comando tf.keras.Sequential indica que vamos criar várias camadas uma ligada na outra. O comando tf.keras.layers.Dense indica que a camada que vamos criar uma camada composta apenas de neurônios.
Como usamos tf.keras.Sequential precisamos indicar as camadas na ordem que elas devem ser criadas. A primeira camada foi criada informando que ela deva ser construída usando: units=5, para indicar que esta camada tem 5 neurônio (como apresentado na Figura 1); activation=”tanh”, para indicarmos que estamos usando a função de ativação Tangente Hiperbólica em todos os neurônios desta camada; input_shape=(3,), para indicar que teremos 3 (três) valores de entradas (que correspondem aos 3 sensores do robô); e name=”Hidden_Layer”, para darmos um nome à camada que neste caso identificamos ela como a camada oculta da rede neural (hidden layer).
Para a camada de saída, seguimos com o mesmo raciocínio. Porém, no caso usamos: units=1, já que a camada de saída deve conter apenas um único neurônio; activation=”tanh”, para, novamente, usarmos a função Tangente Hiperbólica como função de ativação; e name=”Output_Layer”, para darmos um nome a esta camada.
Lembrando que essa rede neural está descrita no objeto model, podemos verificar as características construtivas dela com o comando:
model.summary()
Para finalizarmos a construção da rede neural, precisamos informar qual técnica ela deve utilizar para aprender. Neste caso, vamos utilizar o método compile da nossa rede neural model:
model.compile(optimizer='adam',
loss='mae')
Aqui o optimizer=’adam’ indica qual técnica a rede neural irá utilizar para otimizar o resultado. O termo adam se refere à técnica de otimização estocástica de descida de gradiente, em outras palavras, como a rede neural vai alterar os pesos para minimizar o erro na sua saída.
Como métrica para a avaliação do erro estamos utilizando loss= ‘mae’. A métrica mae se refere à média dos erros absolutos, sendo o objetivo chegar no menor erro possível. A equação da métrica mae é descrita como:
loss = \left | y_{true} - y_{pred} \right |Em que:
- loss é o valor do erro e o valor a ser minimizado, aproximado de zero;
- y_{true} é o valor real, sendo aquele que deve ser indicado pela rede neural;
- y_{pred} é o valor indicado pela rede neural quando enviamos os dados para ela.
Basicamente, estamos falando para a rede neural que, durante o seu treinamento, ela deve testar possíveis leituras dos sensores e encontrar uma resposta. Esta resposta será confrontada com a resposta correta. A diferença entre a resposta correta e a resposta obtida pela rede neural é o que chamamos de erro. Por fim, o otimizador adam irá trabalhar alterando os pesos (os valores de w_i) de forma que o valor de loss vá diminuindo.
Agora que temos uma rede neural semelhante à do robô, precisamos treiná-la para que ela seja capaz de controlar o robô de forma adequada. Porém, para treinar realizar o treinamento precisamos de um conjunto de dados.
Criando um conjunto de dados para treinar a rede neural
O robô que iremos treinar possui 3 (três) sensores, eles serão os valores de entrada para a rede neural. Estes sensores irão indicar 1 (um) caso o robô possa ir na direção do sensor e 0 (zero) caso o robô não possa ir na direção do sensor.
Para cada combinação de valores para os sensores, devemos informar um valor de saída para a rede neural, que irão indicar se o robô ou vira para a direita (valor maior do que +0,5 — vamos utiliza +1), ou vira para a esquerda (valor menor do que -0,5 — vamos utiliza -1), ou se ele deve seguir em frente (vamos utiliza 0).
Combinando os valores de entrada da rede neural e de saída dela podemos criar a Tabela 1.
| Sensor da Esquerda | Sensor da Frente | Sensor da Direita | Saída da Rede Neural | Comportamento do Robô |
| 0 | 0 | 0 | -1 | Se não pode segui nem para direita, nem para frente, nem para esquerda, então deve girar para a esquerda |
| 0 | 0 | 1 | 1 | Se só há caminho para direita, então deve girar para a direita |
| 0 | 1 | 0 | 0 | Se só há caminho para frente, então deve seguir em frente |
| 0 | 1 | 1 | 0 | Se há caminho para frente e para direita, então deve seguir em frente |
| 1 | 0 | 0 | -1 | Se só há caminho para a esquerda, então deve girar para a esquerda |
| 1 | 0 | 1 | 1 | Se há caminho para a esquerda e para a direita, então deve girar para a direita |
| 1 | 1 | 0 | 0 | Se há caminho para a esquerda e para frente, então deve seguir em frente |
| 1 | 1 | 1 | 0 | Se há caminho para esquerda, para frente e para direita, então deve seguir para frente |
Repare que os valores apresentados na Tabela 1 listam todas as 8 (oito) combinações possíveis de valores informados pelos sensores nas colunas Sensor da Esquerda, Sensor da Frente e Sensor da Direita. Já os valores da coluna Saída da Rede Neural foram escolhidos por mim para que o robô tenha os comportamentos apresentados na coluna Comportamento do Robô. Neste caso, é possível alterar os valores apresentados na Saída da Rede Neural para alterar o comportamento do robô, de acordo com o objetivo que o projetista queira alcançar e tomando os devidos cuidados para que o robô não faça uma ação indesejada.
Seguindo o modelo de comportamento indicado na Tabela 1, podemos descrever os dados de treinamento como:
x_train = [[0,0,0], [0,0,1], [0,1,0], [0,1,1], [1,0,0], [1,0,1], [1,1,0], [1,1,1]] y_train = [[-1], [1], [0], [0], [-1], [1], [0], [0]]
Em que x_train é uma lista que representa os conjunto dos possíveis valores de entrada, o dataset de entrada, e y_train é uma lista que representa o comportamento do robô para cada conjunto de dados de x_train. y_train também é conhecido como dataset de saída.
Agora já temos a rede neural e o dataset. O próximo passo é realizar o treinamento da rede neural para que ela possa interpretar os dados da entrada e informar qual é a saída mais adequada o possível.
Treinando a rede neural com o TensorFlow
Nesta etapa vamos utilizar o TensorFlow para treinar a rede neural. Podemos definir como treinamento da rede neural a variação dos valores dos pesos (ou influência dos neurônios) de uma camada na outra e a variação do bias de tal forma que a rede neural possa indicar a melhor resposta o possível. No nosso caso estamos utilizando a estratégia adam e verificando o erro como mae, como informamos anteriormente.
O treinamento com o TensorFlow pode ser realizado com o comando:
training = model.fit(x_train, y_train,
batch_size=8,
epochs=1000,
)
Conforme indicado, estaremos guardando o resultado do treinamento no objeto training. Para isso iremos pegar o objeto model que descreve a nossa rede neural e solicitar o método fit dele. Como argumentos, estamos indicando x_train e y_train sendo os dados de entrada e os dados de saída; batch_size=8, em que batch_size é a quantidade de dados que vamos jogar na rede neural ao mesmo tempo; epochs=1000, que quer dizer que vamos repetir o treinamento 1.000 vezes para, então, avaliarmos o resultado dela.
A função do batch_size é reduzir o tamanho de datasets muito grande para que não sobrecarregue a memória do computador que irá realizar o treinamento da rede neural. Neste caso, o dataset é pequeno, tendo apenas 8 conjunto de dados possíveis, o que dificilmente irá sobrecarregar o computador que irá realizar o treinamento. Sendo, assim, foi indicado um batch_size=8 que corresponde a usar todo o dataset deste projeto a cada época.
Para acompanharmos o desempenho do treinamento, podemos recorrer a uma análise gráfica da evolução do erro. Isso pode ser feito pelos comandos:
error_chart = np.array(training.history['loss']) plt.plot(error_chart) plt.show()
Como resultado pelo treinamento das primeiras 1.000 épocas, temos o gráfico da evolução do erro apresentado na Figura 2.
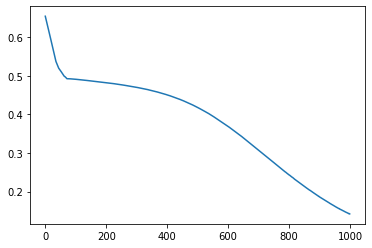
Conforme podemos ver na Figura 2, o erro está sempre diminuindo. Isso indica que ainda há espaço para melhorar o desempenho da rede neural. Essa melhoria pode ser obtida repetindo o processo de treinamento. Após treinarmos por mais 1.000 épocas temos o resultado apresentado na Figura 3.
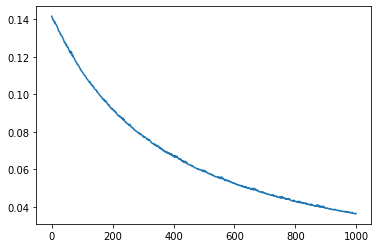
Conforme podemos visualizar na Figura 3, o desempenho do erro está tendendo a chegar em um valor mínimo. Isso pode ser observado pelo formato da curva apresentada. Podemos continuar o treinamento, mais não haverá grandes melhorias no desempenho da rede neural, conforme indicado na Figura 4.
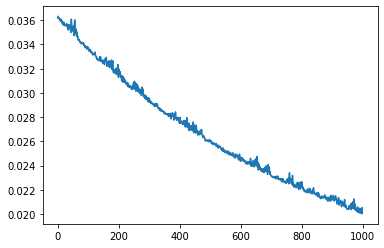
Como podemos visualizar na Figura 4, a melhoria do erro entre a segunda e terceira rodada de treinamento foi muito pequena, tanto que o gráfico começou a ressaltar alguns aumentos no valor do erro durante o treinamento. Isso quer dizer que já estamos chegando ao limite do que essa rede neural é capaz de nos entregar.
Dessa forma, vamos ficar com os resultados que obtivemos após a terceira rodada de treinamentos.
Observação a respeito da quantidade de treinamentos
Quando estamos treinando uma rede neural devemos tomar cuidado para não forçarmos muito o treinamento da rede neural e, ao mesmo tempo, também não treinarmos pouco ela.
Se treinarmos pouco a rede neural chegaremos a um problema chamado de underfit, que corresponde ao fato da rede neural não conseguir apresentar resultados satisfatórios, obtendo uma grande taxa de erro para quais quer valores usados como entrada.
Por outro lado, se treinarmos muito a rede neural chegamos a um problema chamado de overfit, que corresponde ao fato da rede neural apresentar um erro extremamente baixo para os dados de treinamento, mas quando apresentamos novos dados para a rede neural ela apresenta uma taxa de erro elevada. Em outras palavras, podemos dizer que a rede neural “decorou” os dados de treinamento e só consegue trabalhar com eles.
De maneira geral, quando treinamos uma rede neural esperamos que ela também seja capaz de trabalhar com valores distintos aos que foram apresentados a ela durante o treinamento.
No caso específico do controle do robô não existe possibilidade de sinais de entrada diferente dos 8 apresentados na Tabela 1 e, dessa forma, para esta função não haverá problemas no comportamento do robô caso cheguemos à situação de overfit.
Transferindo o aprendizado para o robô
Agora que treinamos uma rede neural que possui as mesmas características do nosso robô, temos que transferir esse aprendizado para ele. Isso é feito informando o peso de cada ligação entre os neurônios e o bias de cada neurônio da rede neural do robô.
Podemos obter os pesos e o bias da primeira camada usando os comandos:
print(model.layers[0].weights) print(model.layers[0].bias.numpy())
[<tf.Variable 'Hidden_Layer/kernel:0' shape=(3, 5) dtype=float32, numpy=
array([[-0.18226664, 0.06532662, 0.21953084, 0.08815249, -0.72672325],
[-1.8973173 , 1.1777258 , -0.6316265 , -2.163294 , 0.34746122],
[ 1.5755405 , 2.321584 , 1.2375892 , -3.493037 , 0.08445551]],
dtype=float32)>, <tf.Variable 'Hidden_Layer/bias:0' shape=(5,) dtype=float32, numpy=
array([-0.6985663 , -0.32421154, 0.40271592, 0.84894747, 0.11173446],
dtype=float32)>]
[-0.6985663 -0.32421154 0.40271592 0.84894747 0.11173446]
Já os pesos e o bias da segunda camada podem ser obtidos com os comandos:
print(model.layers[1].weights) print(model.layers[1].bias.numpy())
[<tf.Variable 'Output_Layer/kernel:0' shape=(5, 1) dtype=float32, numpy=
array([[ 1.7698333 ],
[ 1.1247258 ],
[-0.8695395 ],
[-1.1228516 ],
[-0.26583275]], dtype=float32)>, <tf.Variable 'Output_Layer/bias:0' shape=(1,) dtype=float32, numpy=array([-0.08201659], dtype=float32)>]
[-0.08201659]
Em cada uma das colunas dos resultados temos os valores dos pesos para a entrada de cada neurônio e na ultima linha os bias. Veja que os valores obtidos aqui dependem do treinamento realizado e podem variar entre treinamentos.
De posse dos valores dos pesos e dos bias, no simulador podemos clicar na engrenagem da opção Configuração da IA, apresentada na Figura 5.

Na configuração da IA do robô temos os neurônios. Ao clicarmos neles, podemos informar os pesos de suas entradas e o seu bias, conforme indicado na Figura 6.
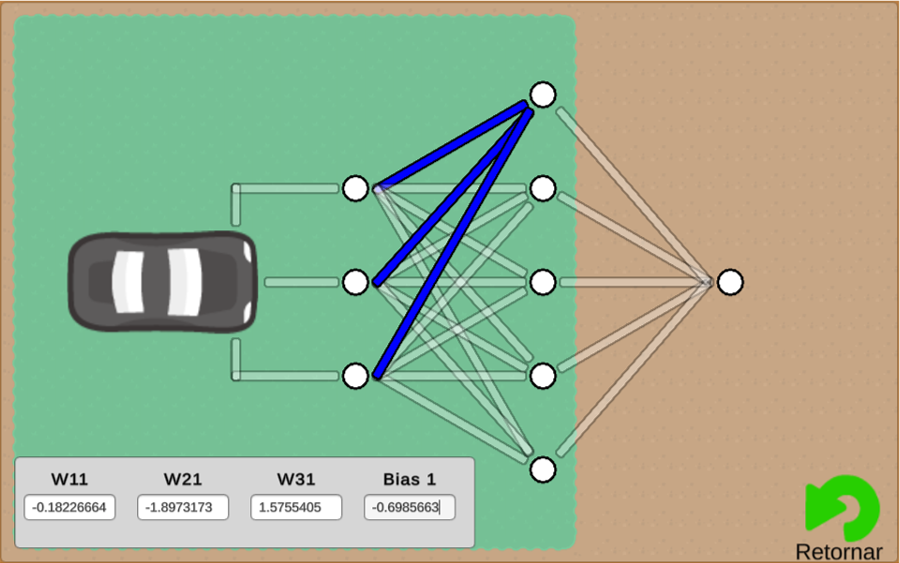
Informado todos os pesos e bias de todos os neurônio podemos desenhar um trajeto que o robô irá seguir. Depois, basta ligarmos o robô e vermos o desempenho dele. Se quisermos, o simulador permite alterarmos o caminho enquanto o robô se movimenta.
Considerações finais
Aqui vimos uma forma de usarmos uma rede neural para controlar o movimento de um robô. Após o treinamento, o simulador permite que informemos os pesos e bias para acompanharmos o resultado e, dessa forma, podemos, também, explorar o que cada peso influencia no comportamento do robô.
No link https://colab.research.google.com/drive/1je9qH_v-oN0s5S2xLDk5r9o3uS_g3jlQ?usp=sharing é possível encontrar o código utilizado para treinar uma rede neural igual a do robô. E, dessa forma, podemos sugerir outros comportamentos para o robô ao alterarmos os valores de y_train.

Faça um comentário